25 Outliers
 Ce chapitre est à l’origine une contribution de kiransaini
Ce chapitre est à l’origine une contribution de kiransaini
En cours de progression. Toute amélioration est la bienvenue. Si vous souhaitez participer rendez vous sur contributing to our repo.
25.1 Vue d’ensemble
Cette section explique quels types d’outliers peuvent être rencontrés dans les données et comment les gérer.
25.2 tl;dr
Je veux voir des outliers!
Les outliers sont difficiles à repérer, car juger qu’un point est un outlier dépend de vos données et du modèle avec lequel il est comparé. Il est important de détecter les outliers car ils peuvent fausser les prévisions et affecter la précision du modèle.
25.3 Que sont outliers?
En un mot, les outliers sont très clairement loin du nuage de points. Il peut s’agir d’erreurs, de véritables valeurs extrêmes, de valeurs rares, de valeurs inhabituelles, de cas présentant un intérêt particulier ou de données provenant d’une autre source. Les outliers d’une variable peuvent être repéré individuellement avec des boxplots et les outliers bi-variables peuvent être repérés avec des scatterplots. Il peut aussi y avoir des outliers de plus grande dimension qui ne sont pas outliers dans les dimensions plus petites.
Cela vaut la peine d’identifier les outliers pour un certain nombre de raisons. Les mauvais outliers doit toujours être corrigé et de nombreuses méthodes statistiques ne peuvent pas bien fonctionner en présence d’outliers. Néanmoins, un bon outlier peut être intéressant. Regardons le outliers du ‘carat’ variable dans le jeu de donnéé ‘diamond’ :
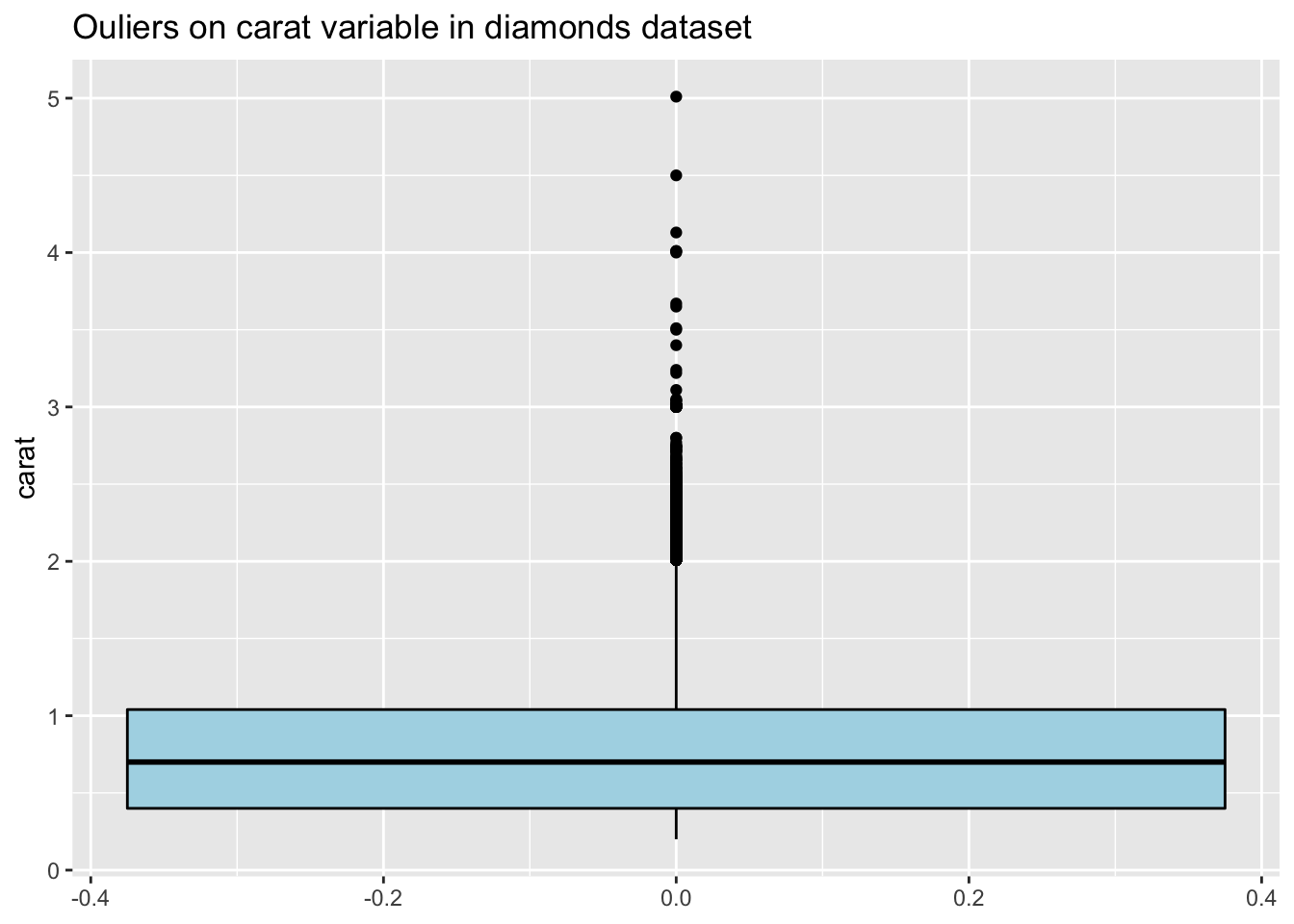
25.4 Types d’outliers
25.4.1 Outliers univariable
Les outliers univariable sont des outliers sur une dimension. L’approche la plus connue pour un premier examen des données consiste à utiliser des boxplots. Tukey suggère de considérer les un point comme outliers s’il est à plus que 1.5 IQR (intervalle inter-quartile) après les lignes (essentiellement le quartiles). Les outliers peuvent changer s’ils sont regroupés avec une autre variable. Examinons les outliers du Sepal.Width variable du jeu de données iris, à la fois lorsque les données sont regroupées par “Species” et quand elles ne le sont pas. Les outliers sont clairement différents :
p <- ggplot(iris, aes(x=Species, y=Sepal.Width)) +
geom_boxplot(color="black", fill="lightblue") +
ggtitle("Boxplot for Sepal Width grouped by Species in iris dataset")
p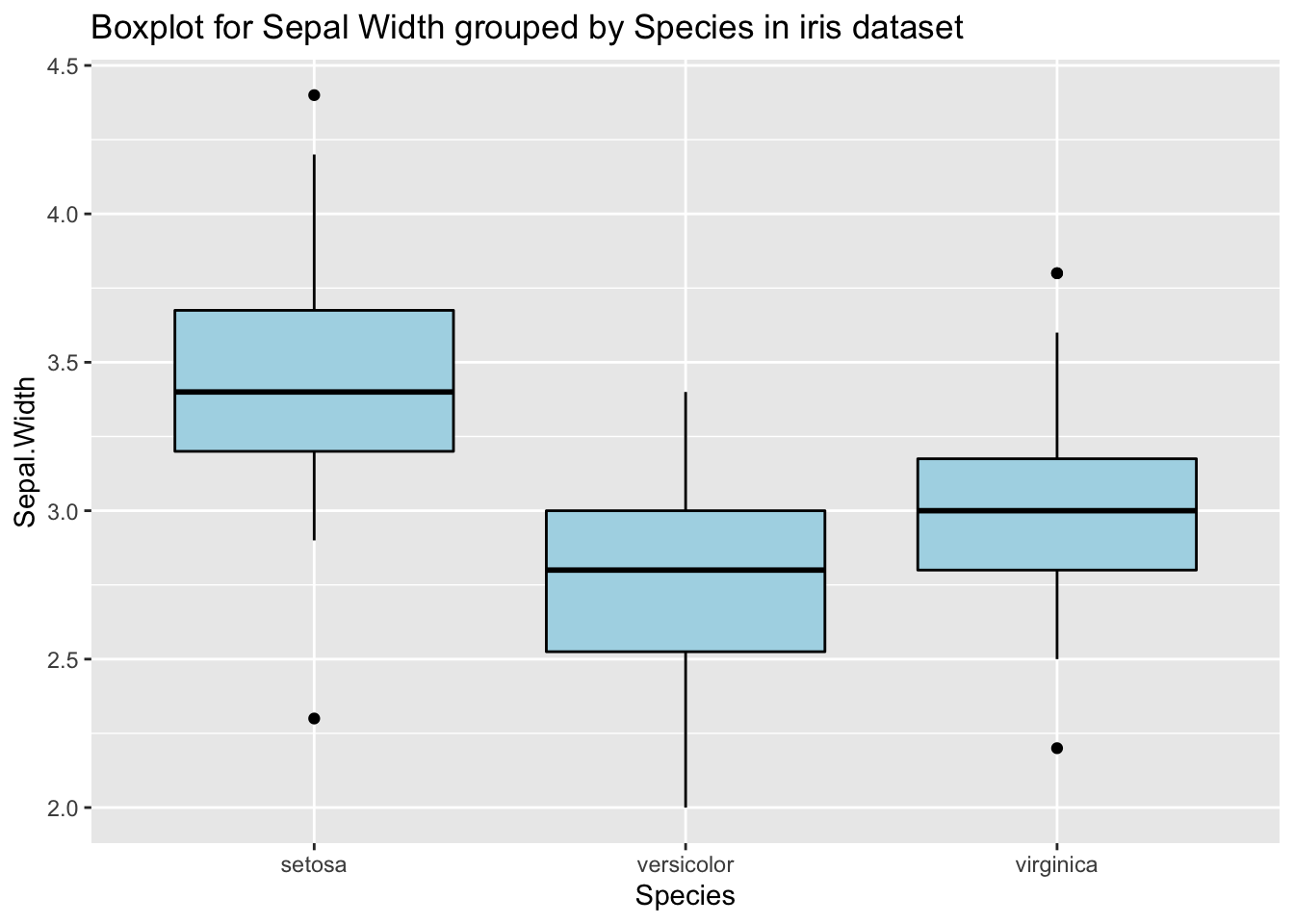
p <- ggplot(iris, aes(y=Sepal.Width)) +
geom_boxplot(color="black", fill="lightblue") +
ggtitle("Boxplot for Sepal Width in iris dataset")
p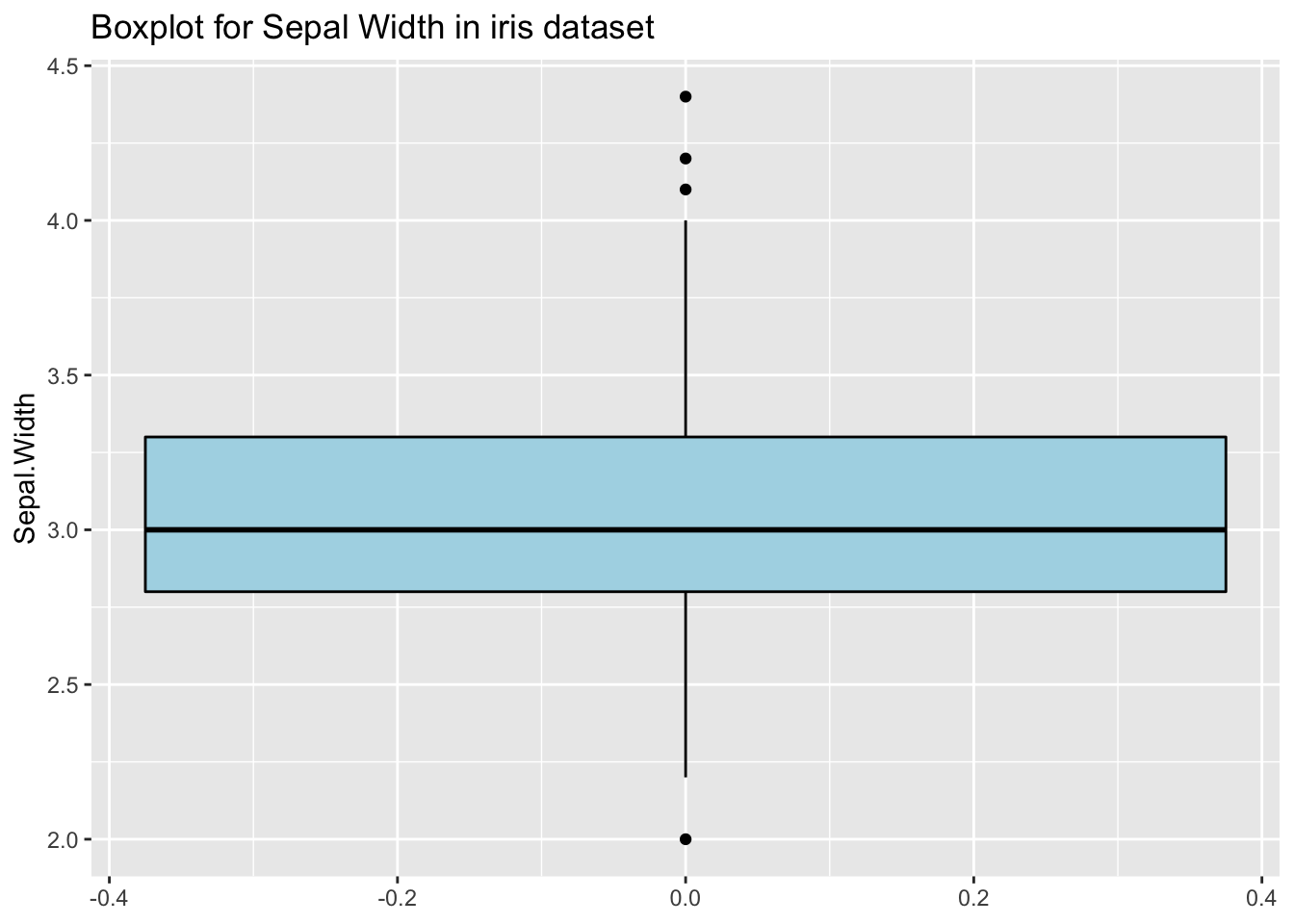
25.4.2 Les outliers multivariables
Les outliers multivariables sont des outliers sur plus d’une dimension. Les scatterplots et parallel coordinate plots sont utiles pour visualiser des outliers multivariables. Vous pouvez considérer comme outlier un point éloigné de la masse ou bien les points ne rentrant pas dans les courbes modélisant le nuage (smooth curve). Certains points sont des outliers sur les deux critères. Regardons outliers sur les variables “Petal.Length” et “Sepal.Width” du jeu de données ‘iris’. Nous pouvons clairement voir un outlier qui est loin de la masse des données (en bas à gauche):
ggplot(iris, aes(x=Sepal.Width, y=Petal.Length)) +
geom_point() +
ggtitle("Scatterplot for Petal Length vs Sepal Width in iris dataset")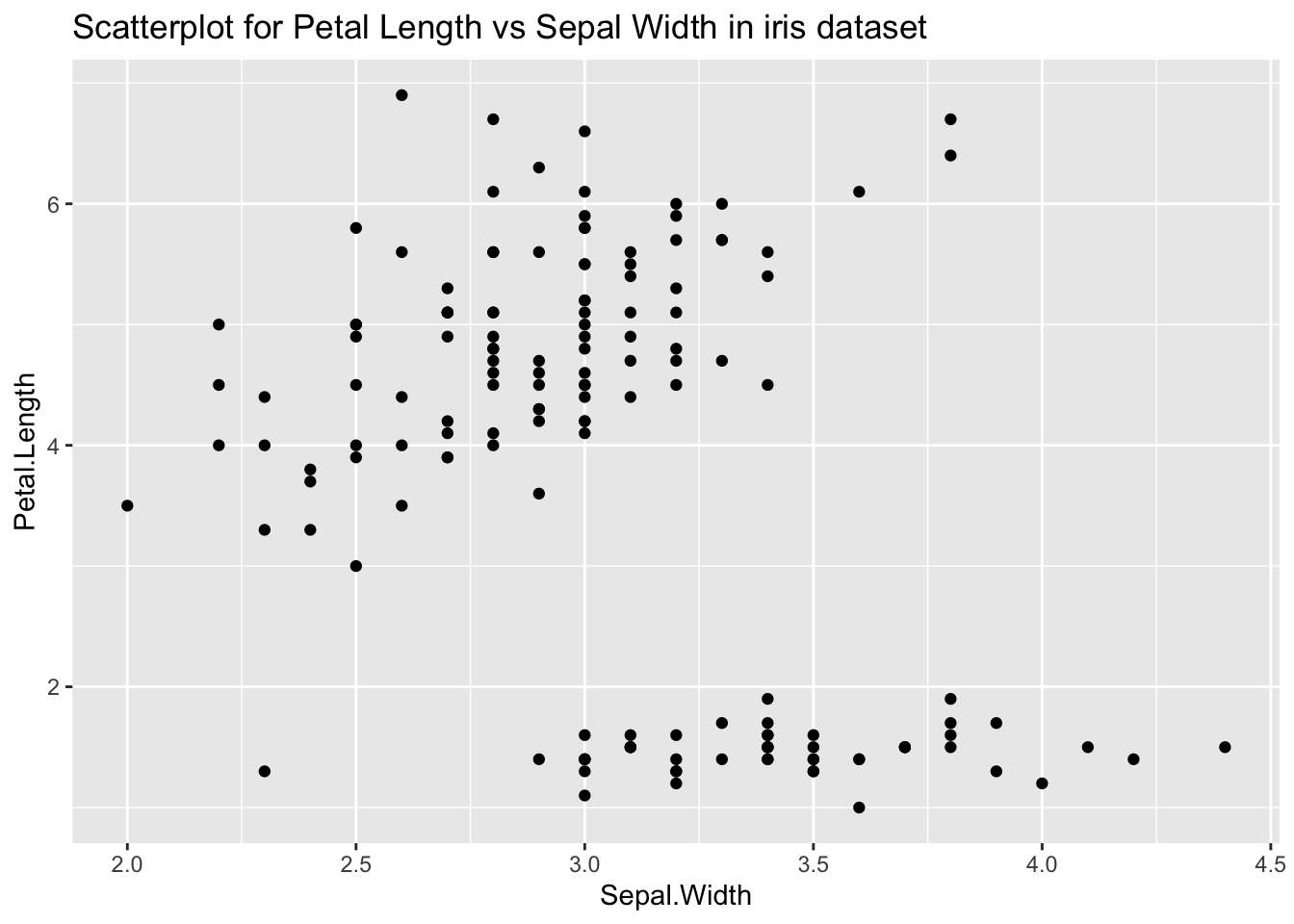
Regardons outliers sur les variables Petal.Length et Petal.Width dans le jeu de données ‘iris’ en ajustant la smooth curve. Ici, les outliers sont les points qui ne sont pas pris dans le smooth model :
ggplot(iris, aes(x=Petal.Width, y=Petal.Length)) +
geom_point() +
geom_smooth() +
geom_density2d(col="red",bins=4) +
ggtitle("Scatterplot for Petal Length vs Petal Width in iris dataset")## `geom_smooth()` using method = 'loess' and formula 'y ~ x'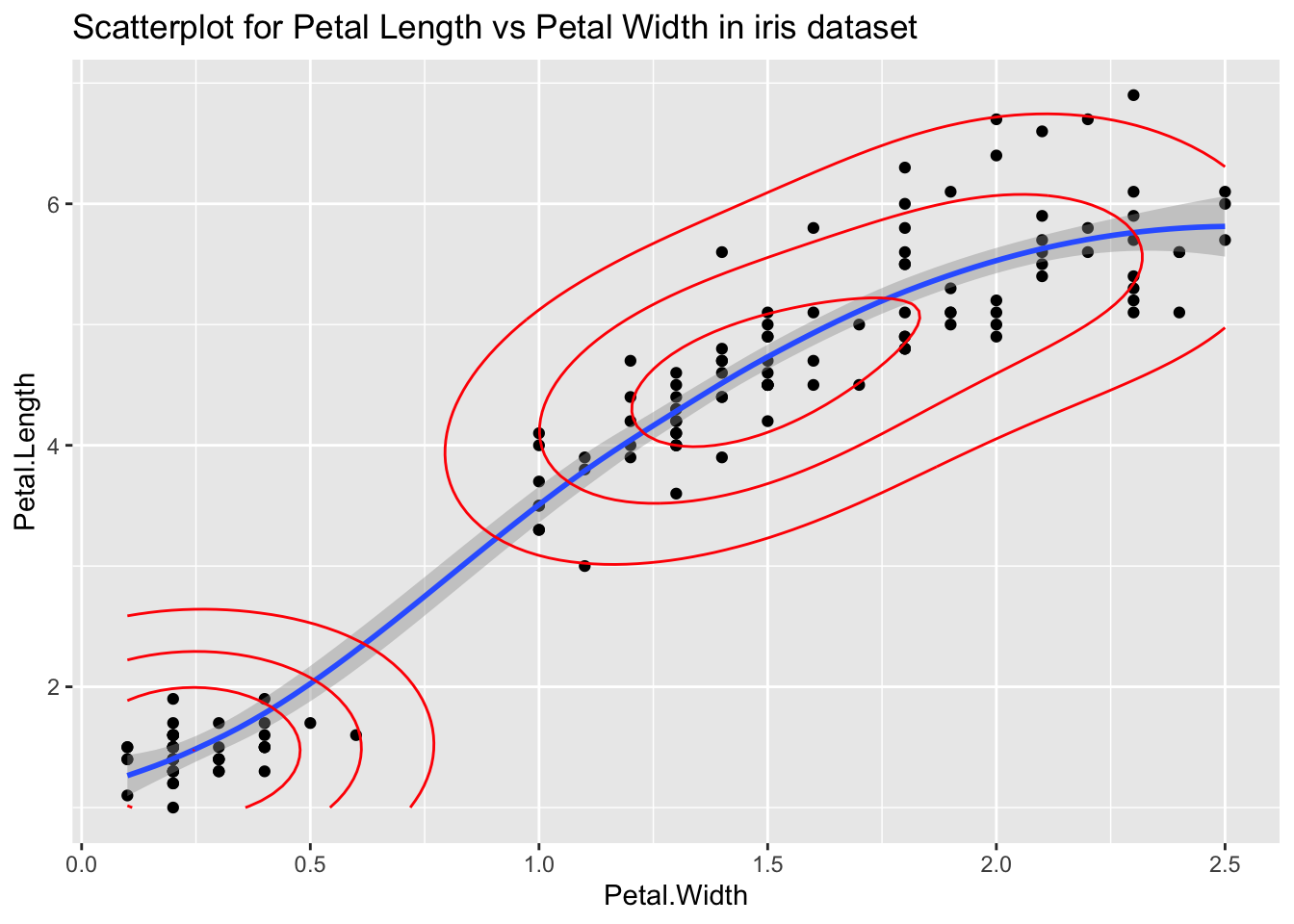
Regardons les outliers dans le jeu de données diamond en utilisant un parallel coordinate plot. Nous pouvons voir un outlier sur les variables carat, cut, color, et clarity qui n’est individuellement un outlier dans aucune des variables :
library(GGally)
ggparcoord(diamonds[1:1000,], columns=1:5, scale="uniminmax", alpha=0.8) +
ggtitle("Parallel coordinate plot of diamonds dataset")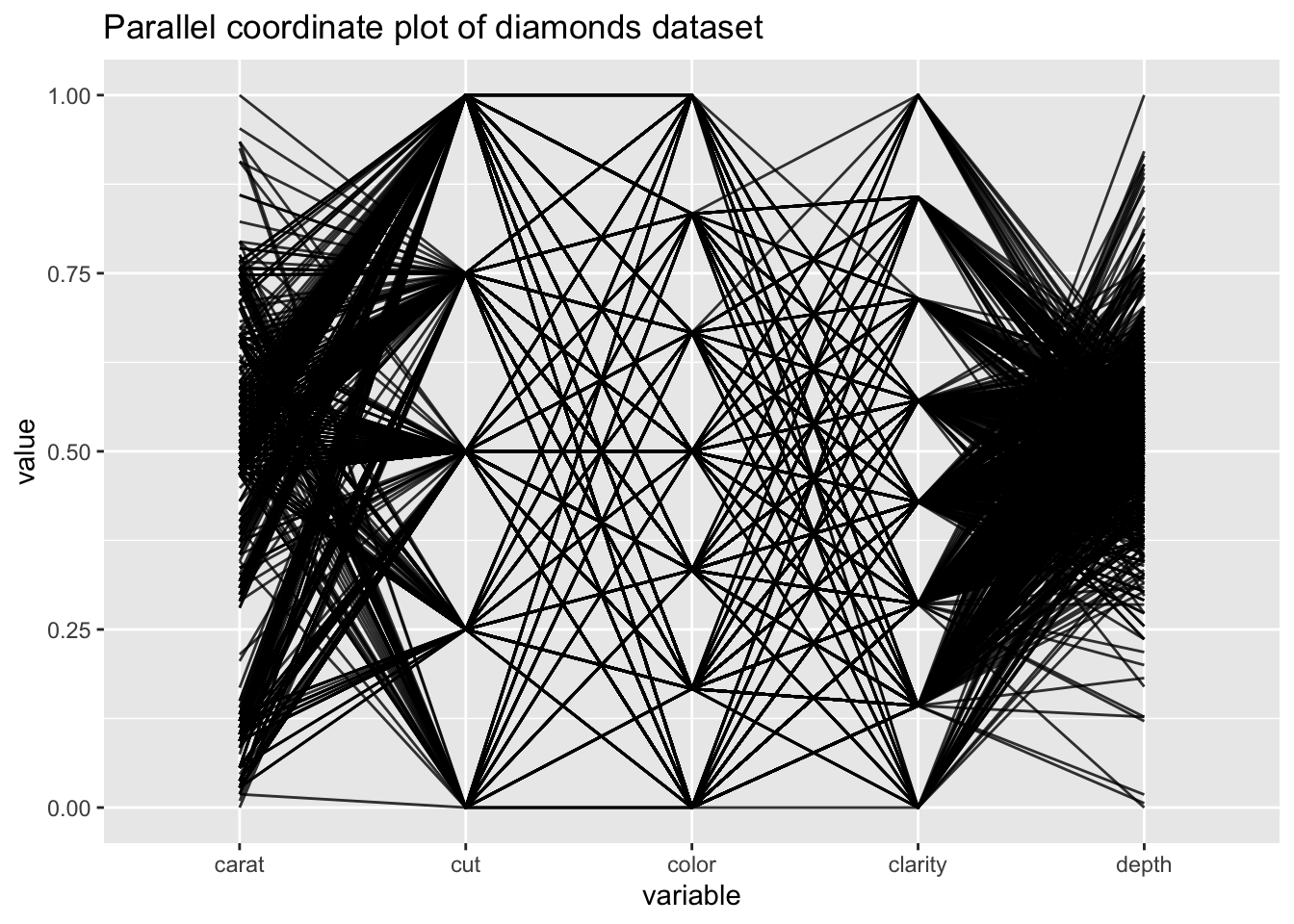
25.4.3 Les outliers catégoriels
Les outliers peuvent être rare sur une échelle catégorielles. Néanmoins, certaines combinaisons de catégories sont rares ou ne devraient pas se produire du tout. Les fluctuation diagrams peuvent être utilisés pour trouver de tels outliers. Nous pouvons à titre d’exemple voir des cas rares dans le jeu de données HairEyeColor :

25.5 Gérer les outliers
Identifier des outlies c’est très facile comparé à ce qu’il faut faire après avoir les avoir identifié. Les outliers peuvent être des cas rares, des valeurs inhabituelles ou de véritables erreurs. Les véritables erreurs doivent être corrigées si possible, sinon elles doivent être supprimées. Retirer des outliers est compliqué et requière des connaissances de base.
Une stratégie pour traiter les outliers est la suivante :
Tracez les distributions 1D des variables en utilisant des boxplots. Examinez toutes les valeurs extremes pour voir si elles sont des valeurs rares ou des erreurs et décider si elles doivent être supprimées ou non.
Pour outliers qui sont des valeurs extremes sur une dimension, examinez leurs valeurs sur d’autres dimensions pour décider si elles doivent être supprimées ou non. Ecartez les valeurs qui sont des outliers sur plusieurs dimensions.
Considérons les cas qui où l’on a un outlier dans une dimension supérieur mais pas dans une dimension inférieure. Déterminez s’il s’agit ou non d’erreurs et envisagez de les éliminer ou pas.
Tracez boxplots et parallel coordinate plots en utilisant le regroupement sur une variable pour trouver outliers dans des sous-ensembles de données.
25.5.1 Sans information
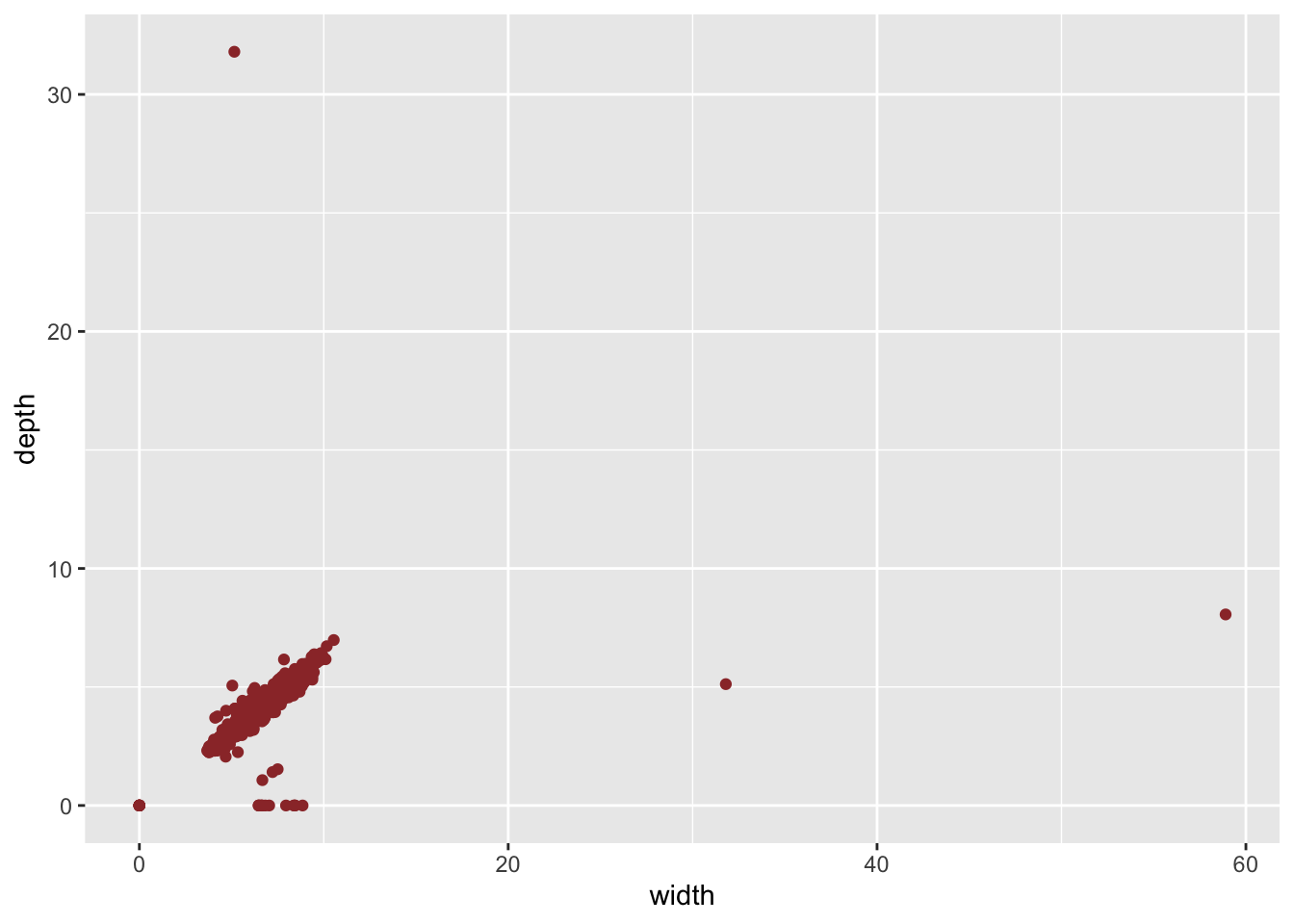
Considérons le jeu de données diamonds. Regardons les variables width (y) et depth (z):
ggplot(diamonds, aes(y=y)) +
geom_boxplot(color="black", fill="#9B3535") +
ggtitle("Ouliers on width variable in diamonds dataset")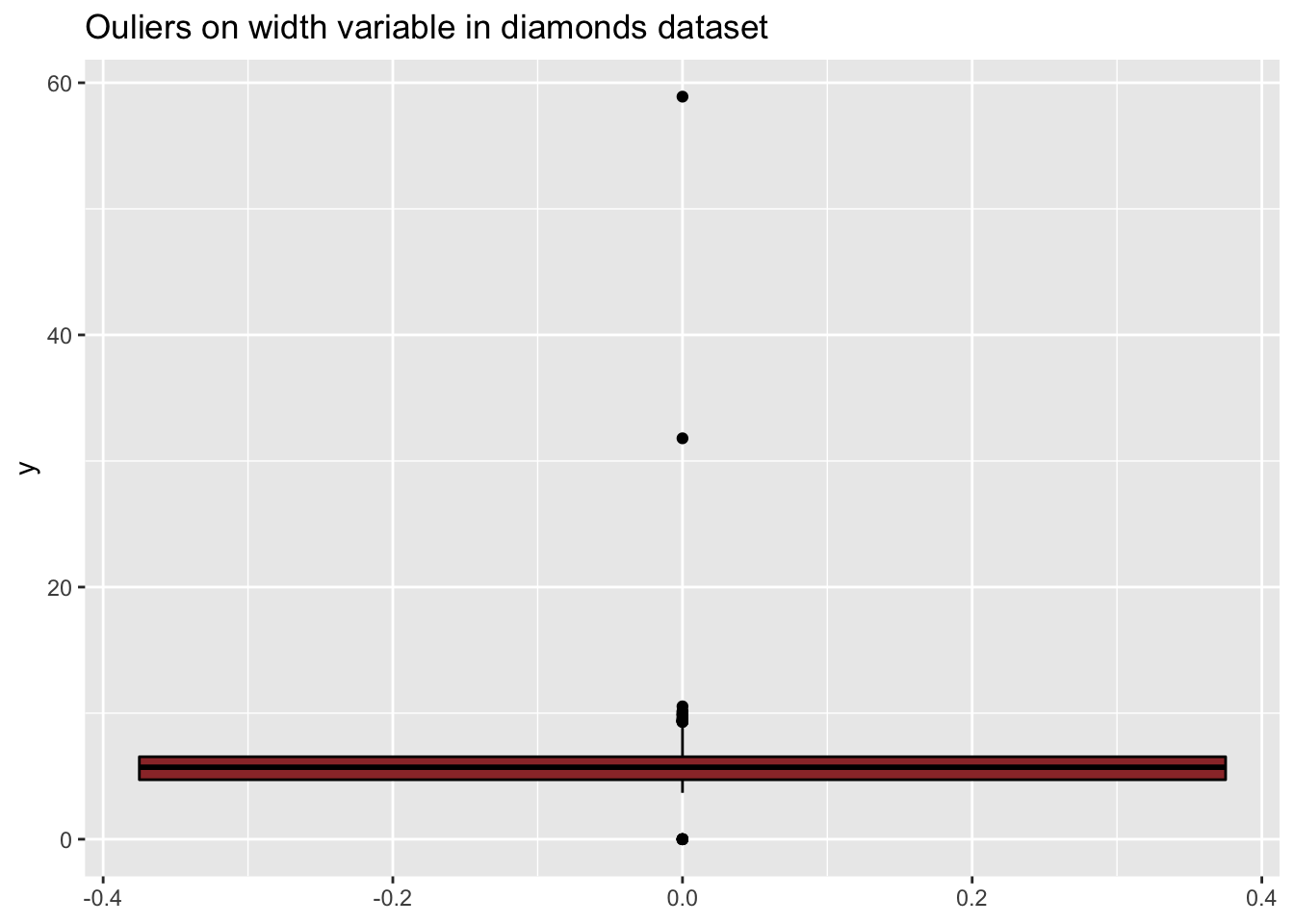
ggplot(diamonds, aes(y=z)) +
geom_boxplot(color="black", fill="#9B3535") +
ggtitle("Ouliers on depth variable in diamonds dataset")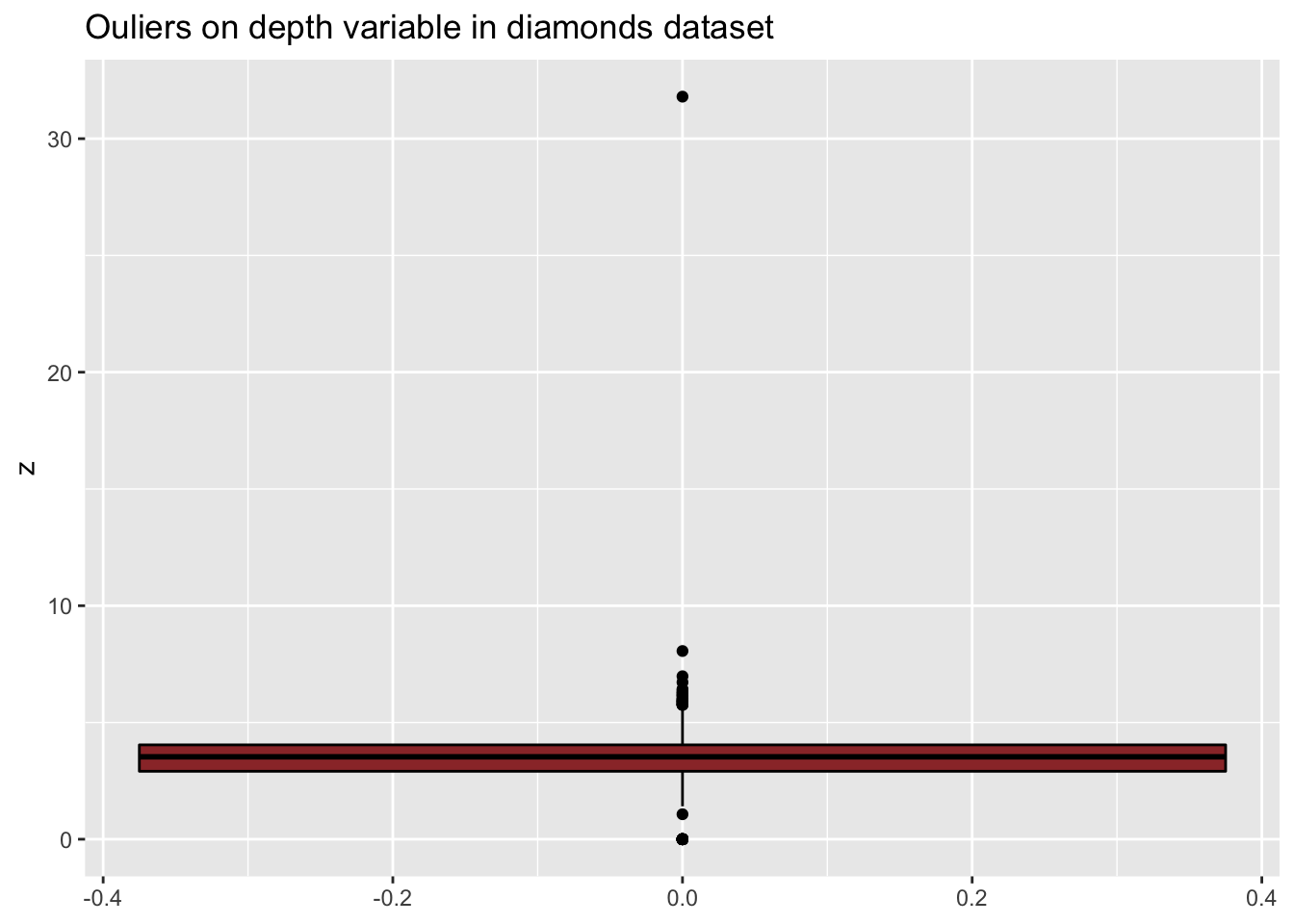
25.5.2 Plus informatif
Les graphiques ne sont pas très informatifs en raison des outliers. Les mêmes graphiques après filtrage des outliers sont beaucoup plus informatifs:
d2 <- filter(diamonds, y > 2 & y < 11 & z > 1 & z < 8)
ggplot(d2, aes(y=y)) +
geom_boxplot(color="black", fill="lightblue") +
ggtitle("Ouliers on width variable in diamonds dataset")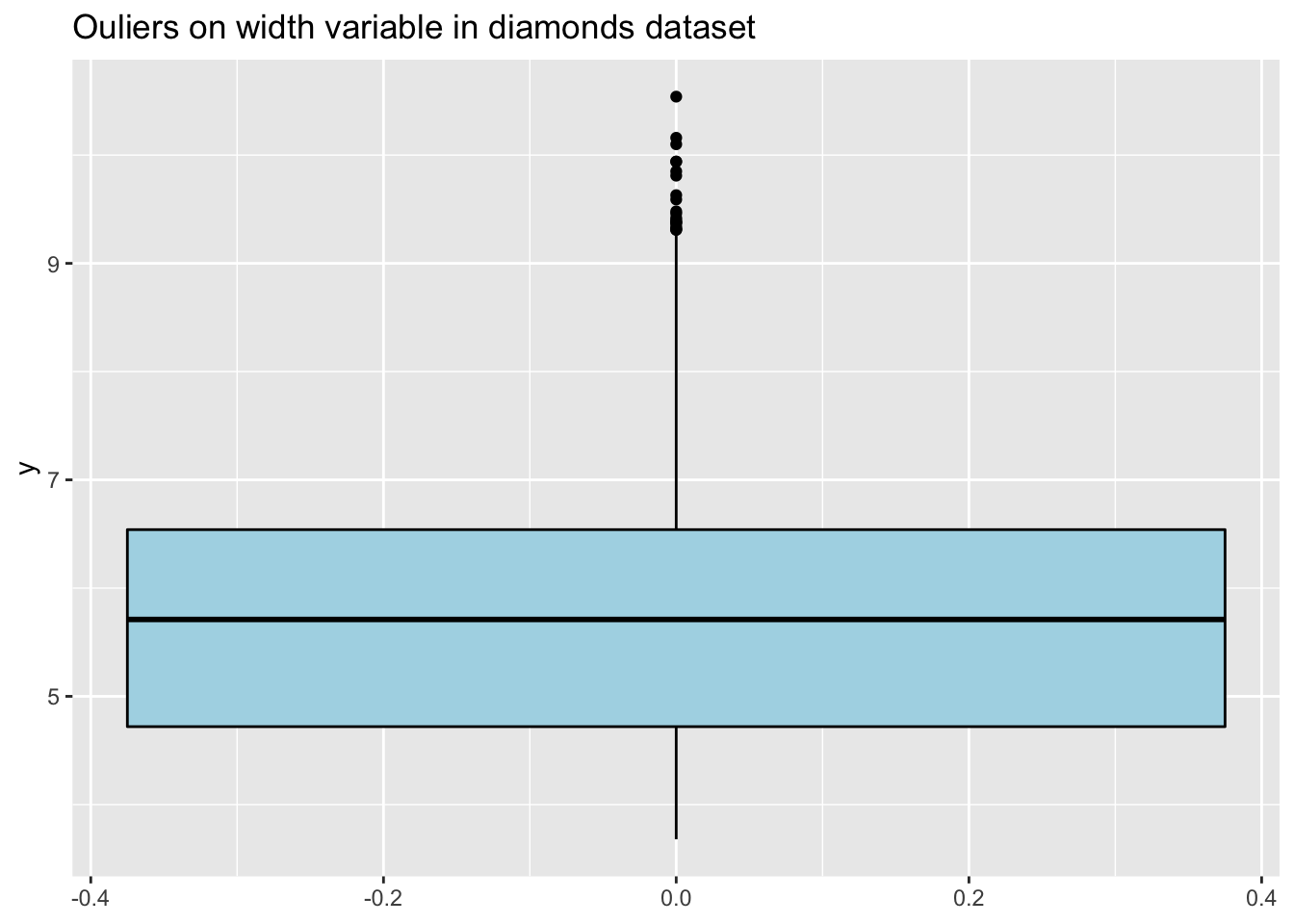
d2 <- filter(diamonds, y > 2 & y < 11 & z > 1 & z < 8)
ggplot(d2, aes(y=z)) +
geom_boxplot(color="black", fill="lightblue") +
ggtitle("Ouliers on depth variable in diamonds dataset")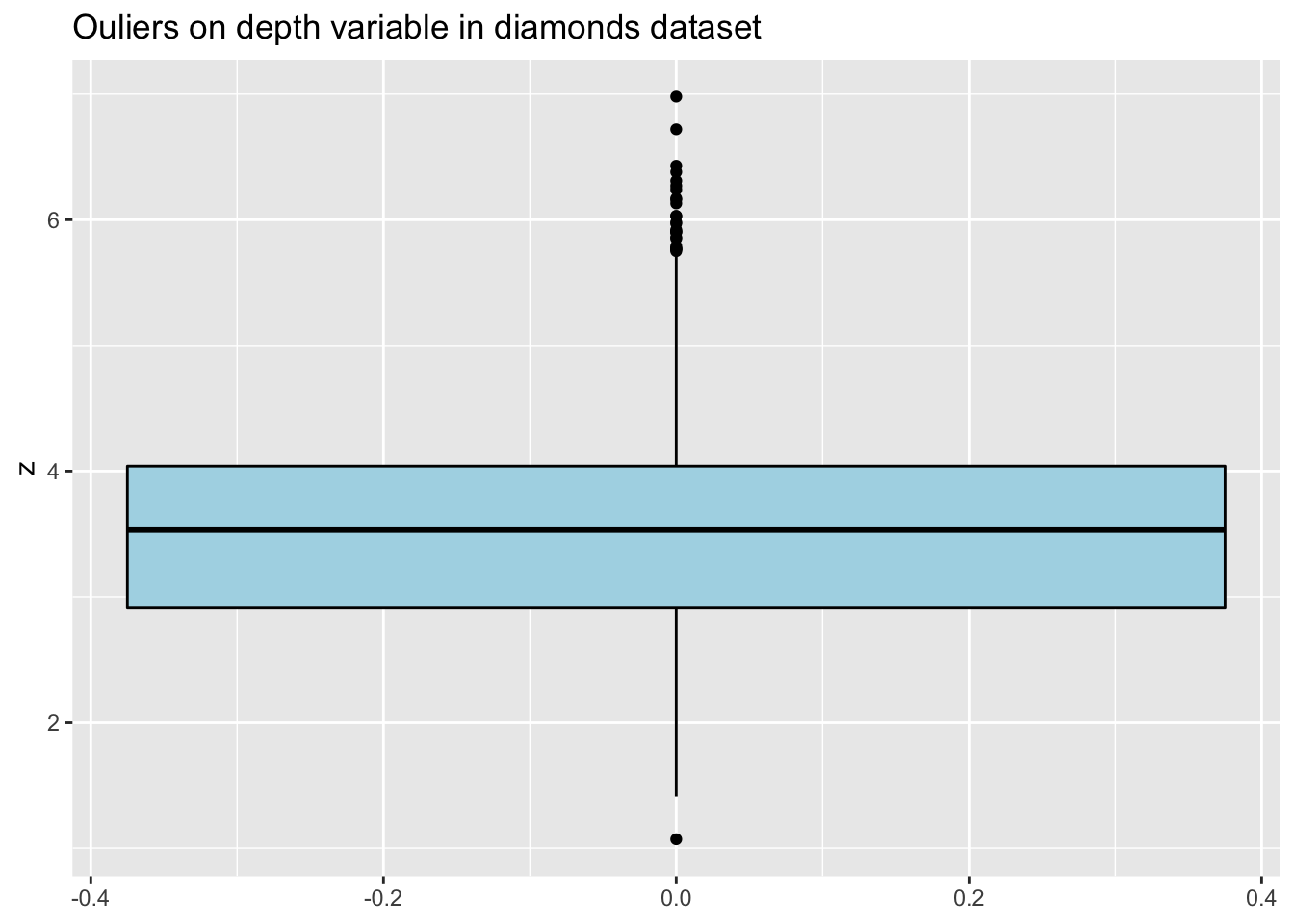
d2 <- filter(diamonds, y > 2 & y < 11 & z > 1 & z < 8)
ggplot(d2, aes(y, z)) +
geom_point(shape = 21, color = "darkGrey", fill = "lightBlue", stroke = 0.1) +
xlab("width") +
ylab("depth")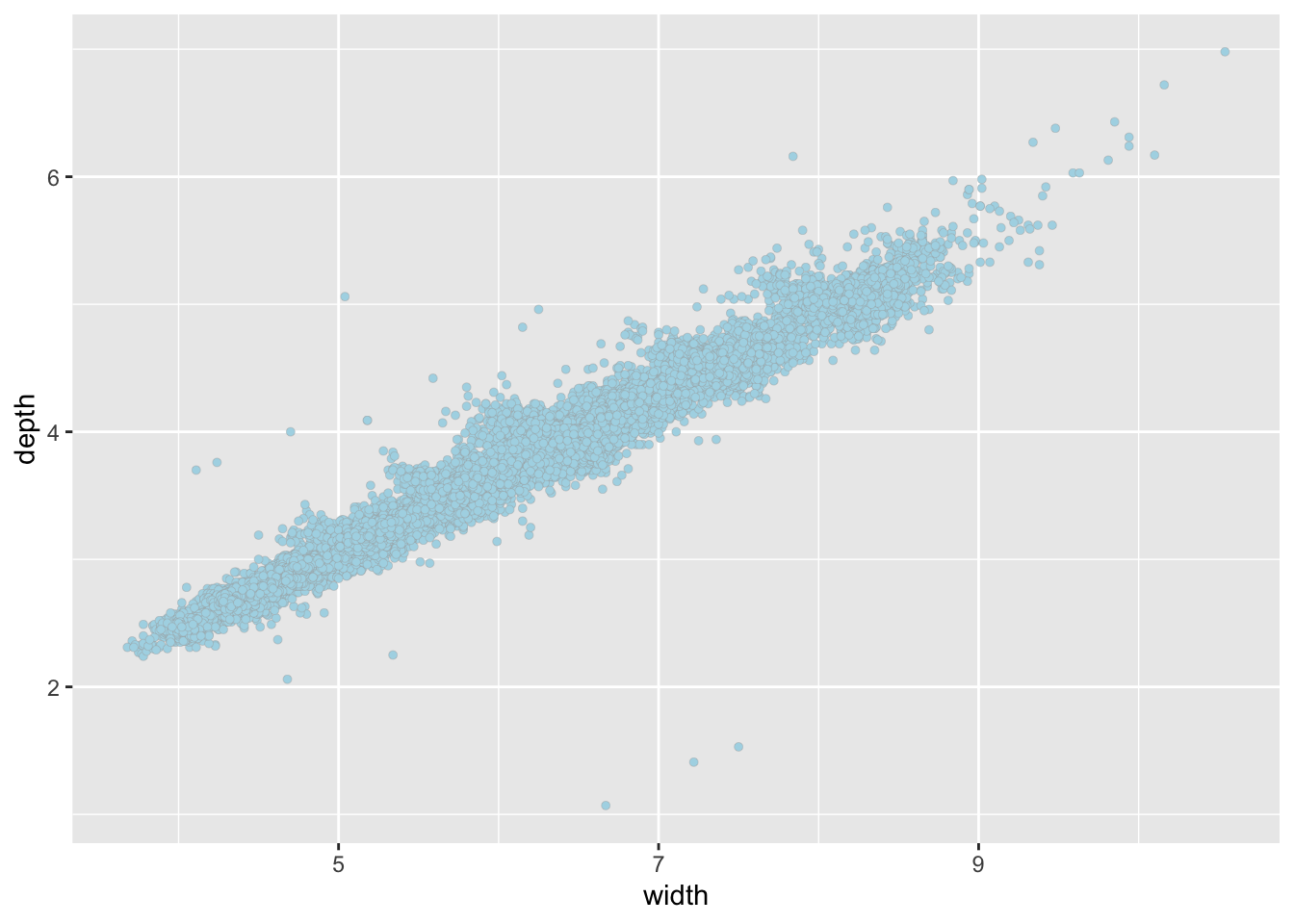
25.6 Ressources externes
Identify, describe, plot, and remove the outliers from the dataset: Afficher et retirer les outliers d’un jeu de données
A Brief Overview of Outlier Detection Techniques: Discussion théorique sur la détection d’outliers.
with